This paper generalizes the definition of a Heegaard splitting to unify the concepts of thin position for 3-manifolds, thin position for knots, and normal and almost normal surface theory. This gives generalizations of theorems of Scharlemann, Thompson, Rubinstein, and Stocking. In the final section, we use this machinery to produce an algorithm to determine the bridge number of a knot, provided thin position for the knot coincides with bridge position. We also present several algorithmic and finiteness results about Dehn fillings with small Heegaard genus.
This paper contains the motivation for the study of critical surfaces in [?]. In that paper, the only justification given for the definition of this new class of surfaces is the strength of the results. However, when viewed as the topological analogue to index 2 minimal surfaces, critical surfaces become quite natural.
In this paper we introduce critical surfaces, which are described via a 1-complex whose definition is reminiscent of the curve complex. Our main result is that if the minimal genus common stabilization of a pair of strongly irreducible Heegaard splittings of a 3-manifold is not critical, then the manifold contains an incompressible surface. Conversely, we also show that if a non-Haken 3-manifold admits at most one Heegaard splitting of each genus, then it does not contain a critical Heegaard surface. In the final section we discuss how this work leads to a natural metric on the space of strongly irreducible Heegaard splittings, as well as many new and interesting open questions.
If a tangle, K ⊂ B3, has no planar, meridional, essential surfaces in its exterior then thin position for K has no thin levels.
Kneser-Haken Finiteness asserts that for each compact 3-manifold M there is an integer c(M) such that any collection of k > c(M) closed, essential, 2-sided surfaces in M must contain parallel elements. We show here that if M is closed then twice the number of tetrahedra in a (pseudo)-triangulation of M suffices for c(M).
We present a complete proof of Theorem 6.3 from “Heegaard splittings with boundary and almost normal surfaces [Topology and Appl. 116(2001) 153-184].” We also take this opportunity to correct a few minor errors that appeared in that paper.
We show if M is a closed, connected, orientable,
hyperbolic 3-manifold with Heegaard genus g then
g ≥ 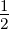 cosh(r) where r denotes the radius of any
isometrically embedded ball in M. Assuming an
unpublished result of Pitts and Rubinstein improves
this to g ≥
cosh(r) where r denotes the radius of any
isometrically embedded ball in M. Assuming an
unpublished result of Pitts and Rubinstein improves
this to g ≥ 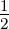 cosh(r) +
cosh(r) + 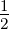 . We also give an upper
bound on the volume in terms of the flip distance of a
Heegaard splitting, and describe isoperimetric surfaces
in hyperbolic balls.
. We also give an upper
bound on the volume in terms of the flip distance of a
Heegaard splitting, and describe isoperimetric surfaces
in hyperbolic balls.
J. Hempel’s definition of the distance of a Heegaard surface generalizes to a complexity for a Heegaard surface with respect to a knot which is in bridge position. Our main result is that the distance of the Heegaard splitting with respect to the knot is bounded above by twice the genus, plus the number of boundary components, of an essential surface in the knot complement. As a consequence knots constructed via sufficiently high powers of pseudo-Anosov maps have minimal bridge presentations which are thin.
This paper studies Heegaard splittings of surface bundles via the curve complex of the fibre. The translation distance of the monodromy is the smallest distance it moves any vertex of the curve complex. We prove that the translation distance is bounded above in terms of the genus of any strongly irreducible Heegaard splitting. As a consequence, if a splitting surface has small genus compared to the translation distance of the monodromy, the splitting is standard.
We show that if two 3-manifolds with toroidal boundary are glued via a “sufficiently complicated” map then every Heegaard splitting of the resulting 3-manifold is weakly reducible. Additionally, suppose X ∪F Y is a manifold obtained by gluing X and Y , two connected small manifolds with incompressible boundary, along a closed surface F. Then the following inequality on genera is obtained:
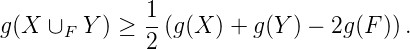
Both results follow from a new technique to simplify the intersection between an incompressible surface and a strongly irreducible Heegaard splitting.
We find a geometric invariant of isotopy classes of strongly irreducible Heegaard splittings of toroidal 3-manifolds. Using this invariant, we show that a closed, totally orientable Seifert fibered space M has infinitely many isotopy classes of Heegaard splittings of the same genus if and only if M has an irreducible, horizontal Heegaard splitting, has a base orbifold of positive genus, and is not a circle bundle. This characterizes precisely which Seifert fibered spaces satisfy the converse of Waldhausen’s conjecture.
We survey known (and unknown) results about the behavior of Heegaard genus of 3-manifolds constructed via various gluings. The constructions we consider are (1) gluing together two 3-manifolds with incompressible boundary, (2) gluing together the boundary components of surface × I, and (3) gluing a handlebody to the boundary of a 3-manifold. We detail those cases in which it is known when the the Heegaard genus is less than what is expected after gluing.
Let M1 and M2 be closed, orientable 3-manifolds. Let Hi denote a Heegaard surface in Mi. We prove that if H1#H2 comes from stabilizing a lower genus splitting of M1#M2 then one of H1 or H2 comes from stabilizing a lower genus splitting. This answers a question of C. Gordon (Problem 3.91 from [?]). We also show that every unstabilized Heegaard splitting has a unique expression as the connected sum of Heegaard splittings of prime 3-manifolds.
The disk complex of a surface in a 3-manifold is used to define its topological index. Surfaces with well-defined topological index are shown to generalize well known classes, such as incompressible, strongly irreducible, and critical surfaces. The main result is that one may always isotope a surface H with topological index n to meet an incompressible surface F so that the sum of the indices of the components of H \ N(F) is at most n. This theorem and its corollaries generalize many known results about surfaces in 3-manifolds, and often provides more efficient proofs. The paper concludes with a list of questions and conjectures, including a natural generalization of Hempel’s distance to surfaces with topological index ≥ 2.
The topological index of a surface was previously introduced by the first author as the topological analogue of the index of an unstable minimal surface. Here we show that surfaces of arbitrarily high topological index exist.
Let M1 and M2 be compact, orientable 3-manifolds with incompressible boundary, and M the manifold obtained by gluing with a homeomorphism ϕ : ∂M1 → ∂M2. We analyze the relationship between the sets of low genus Heegaard splittings of M1, M2, and M, assuming the map ϕ is “sufficiently complicated.” This analysis yields counter-examples to the Stabilization Conjecture, a resolution of the higher genus analogue of a conjecture of Gordon, and a result about the uniqueness of expressions of Heegaard splittings as amalgamations.
We show that a strongly irreducible and boundary-strongly irreducible surface can be isotoped to be almost normal in a triangulated 3-manifold.
We show that after generic filling along a torus boundary component of a 3-manifold, no two closed, 2-sided, essential surfaces become isotopic, and no closed, 2-sided, essential surface becomes inessential. That is, the set of essential surfaces (considered up to isotopy) survives unchanged in all suitably generic Dehn fillings. Furthermore, for all but finitely many non-generic fillings, we show that two essential surfaces can only become isotopic in a constrained way.
Let M be a 3-manifold with torus boundary components T1 and T2. Let ϕ : T1 → T2 be a homeomorphism, Mϕ the manifold obtained from M by gluing T1 to T2 via the map ϕ, and T the image of T1 in Mϕ. We show that if ϕ is “sufficiently complicated” then any incompressible or strongly irreducible surface in Mϕ can be isotoped to be disjoint from T. It follows that every Heegaard splitting of a 3-manifold admitting a “sufficiently complicated” JSJ decomposition is an amalgamation of Heegaard splittings of the components of the JSJ decomposition.
We show that Heegaard Genus ≤ g, the problem of deciding whether a triangulated 3-manifold admits a Heegaard splitting of genus less than or equal to g, is NP-hard. The result follows from a quadratic time reduction of the NP-complete problem CNF-SAT to Heegaard Genus ≤ g.
A topologically minimal surface may be isotoped into a normal form with respect to a fixed triangulation. If the intersection with each tetrahedron is simply connected, then the pieces of this normal form are triangles, quadrilaterals, and helicoids. Helical pieces can have any number of positive or negative twists. We show here that the net twisting of the helical pieces of any such surface in a given triangulated 3-manifold is bounded.